Wat is een grafiek
Een grafiek is een grafische voorstelling van cijfergegevens uit onderzoekingen, resultaten van metingen,
opiniepeilingen, … .
Waarom een grafiek gebruiken?
Een grafische voorstelling is veel overzichtelijker dan een hele tabel met gegevens. Verder is dit de
geknipte manier om te laten zien dat er een evolutie zit in de cijfergegevens. Bovendien is het vrijwel
onmogelijk om in een tabel een evolutie of een verandering te ontdekken, terwijl die in een grafiek meestal
onmiddellijk opvalt.
Algemeen
Tijd en temperatuur zijn grootheden.
De temperatuur hangt af van het tijdstip op de dag: bij een zeker tijdstip hoort een bepaalde temperatuur.
De grafiek geeft het verband aan tussen de twee grootheden.
tijd staat op de horizontale as.
temperatuurstaat op de verticale as.
Je kunt het verloop van de grafiek beschrijven met de woorden: stijgen, dalen en constant.
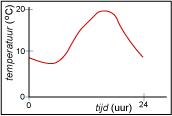
Deze grafiek laat zien:
's nachts daalt de temperatuur, maar vanaf ongeveer 6:00 uur 's morgens begint hij te stijgen. Dat gaat door tot ongeveer 16:00 uur en dan blijft hij even redelijk constant en vanaf 18:00 gaat hij snel dalen.
Grafieken lezen:
Je kunt uit deze grafiek aflezen wat de temperatuur om 7:00 uur was.
- Zoek op de horizontale as 7:00 uur op.
- Ga recht omhoog tot je bij de grafiek bent.
- Lees op de verticale as de temperatuur af.
- Je ziet dat het om 7:00 uur ongeveer 9 °C was.
Grafieken tekenen:
Bij een tabel zoals deze kun je een grafiek tekenen.
|
tijd (uur) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
temperatuur (°C) |
6 |
4 |
3 |
5 |
7 |
11 |
15 |
20 |
24 |
19 |
16 |
12 |
7 |
De temperatuur hangt af van de tijd op de dag.
Dus komt temperatuur op de verticale as en tijd op de horizontale as.
- Teken een assenstelsel. Zet bij de assen wat je
meet (grootheid) en met welke maat (eenheid).
Maak een geschikte indeling voor de assen.
Teken de punten uit de tabel in de grafiek.
- Verbind de punten door een vloeiende kromme,
een curve.
Soorten grafieken of diagrammen
Staafdiagram
Een staafdiagram is een diagram waarin met de lengte van staven een bepaalde waarde duidelijk wordt gemaakt.
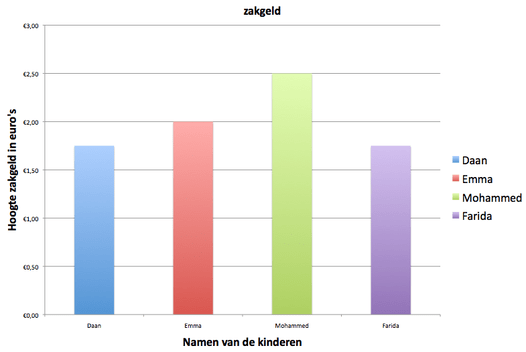
In het staafdiagram hieronder zie je de hoogte van het zakgeld van vier kinderen. Elke staaf geeft de hoogte aan van het zakgeld. Op de horizontale lijn staan de namen van de kinderen. Op de verticale lijn staan de bedragen in euro's. De verticale as begint met het bedrag van 0 euro. En loopt door tot en met 3 euro.
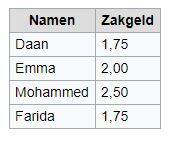
In de tabel ernaast staan de gegevens waarmee het staafdiagram is gemaakt. Je kunt dus letterlijk aflezen hoeveel zakgeld elk kind krijgt.
BEREKENING
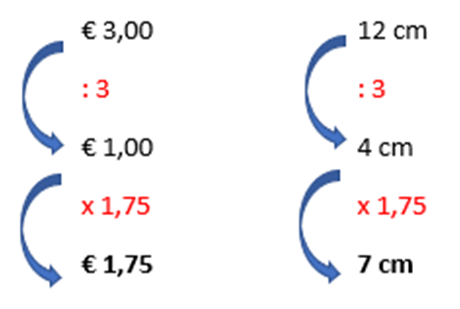
Als je deze grafiek zelf zou moeten tekenen op een leeg rooster , dan zorg je eerst op de verticale as (links naar boven) voor een ijking (een zelf gekozen indeling) zoals hier om de 2 cm een 0.50 euro aanduiden.
Daarna meet je de afstand in cm van de nul euro € 0.00 tot boven aan de € 3,00, dat zou hier 12 cm zijn.
De 'regel van drie' wordt bv voor Daan met zakgeld € 1,75:
Lijndiagram
Een lijndiagram is een diagram waarin met een lijn duidelijk wordt gemaakt hoe onderwerpen zich tot elkaar verhouden. In de lijndiagram staan punten die met een lijn aan elkaar zijn verbonden.
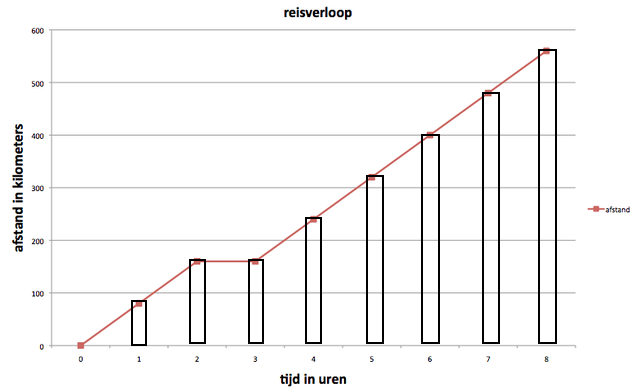
Eigenlijk is eenlijndiagram en de berekeningen die je daarvoor moet doen, net dezelfde als die voor een staafdiagram. Want de puntjes van de lijn zijn de bovenkant van de staaf, net op dezelfde afstand dus.
(zie verkleinde afbeelding eronder)
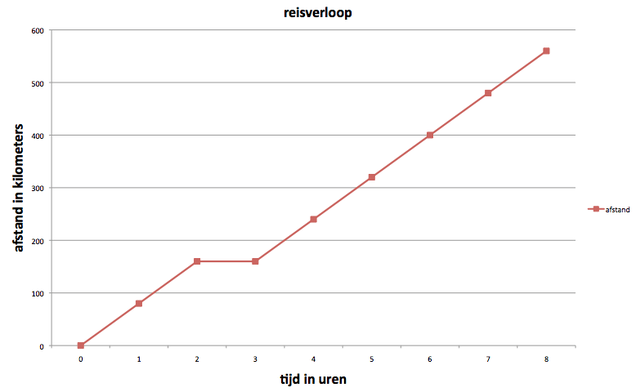
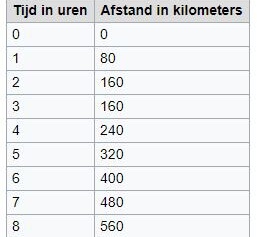
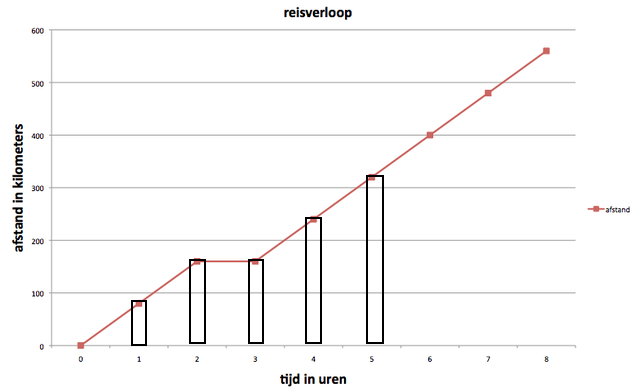
In de grafiek hieronder zie je dat op de horizontale lijn de tijd uitgedrukt in uren staan. De de verticale lijn zie je de afstand staan in kilometers. De lijn van de grafiek geeft het reisverloop aan. Na twee uur reizen is 160 kilometer afgelegd. Tussen de 2 en 3 uur wordt er niet gereisd maar gerust. De lijn stijgt daarom niet. Na 6 uur is er 400 kilometer gereisd. En na 8 uur is dat 560 kilometer.
In de tabel ernaast zie je de getallen waarop de grafiek is gebaseerd.
Cirkeldiagram
Een cirkeldiagram is een diagram waar door middel van een cirkel duidelijk wordt hoe onderwerpen zich met elkaar verhouden.
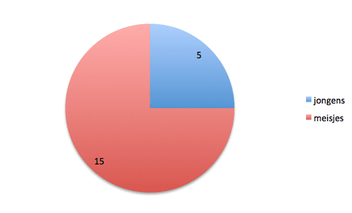
Hieronder zie je twee cirkeldiagrammen die met een afbeelding laten zien hoe de verhouding is tussen het aantal jongens en meisjes in de klas. De totale klas bestaat uit 20 leerlingen.
In de linker cirkeldiagram staan in de twee vlakken de precieze getallen, er zijn 5 jongens en 15 meisjes.
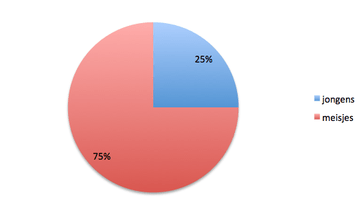
In de rechter cirkeldiagram zie je de percentages staan, 25% bestaat uit jongens, en 75% bestaat uit meisjes.
Een cirkeldiagram helpt met een tekening de verhouding van verschillende getallen in beeld te brengen.
BEREKENING
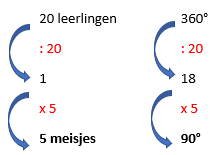
Als je deze linkse grafiek zou tekenen in een leeg cirkeldiagram dan weet je dat de volledige cirkel 360° is.
De 'regel van drie' wordt bv voor de 5 meisjes tov de klas van 20:
Als je deze rechts grafiek zou tekenen in een leeg cirkeldiagram maar nu met % i.p.v. aantal leerlingen.
De 'regel van drie' wordt bv voor de 75 % jongens tov de crikel:
Balk, strook of stapeldiagram
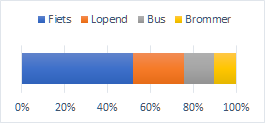
Een strookdiagram is een diagram waarin met de lengte van een onderdeel een bepaalde waarde duidelijk wordt gemaakt tov de totale balk of strook.
BEREKENING
Als je deze grafiek zelf zou moeten tekenen op een leeg rooster , dan zorg je eerst de volledige balk moeten meten.
Stel dat de balk hier 18 cm zoiu zijn.
En als je weet dat de vier onderdelen respctievelijk in procentueel aandeel de volgende waarden hebben:
Fiets => 54 % Lopen => 22 % Bus= > 15 % Brommer => 9 %
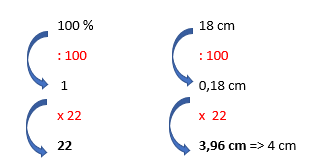
De 'regel van drie' wordt bv voor Lopen :
Even
oefenen
Indien je zelf wil oefenen, hieronder staan 2 opdrachten.
Neem een foto van je resultaat samen met je berekeningen en mail die via Smartschool naar je leerkracht door.
1*
Teken het strookdiagram met de gegeven afmeting en de bijhorende uren van de dagen van de week

2
* Teken het staafdiagram met de onderstaande gegevens:
Een overzicht van waarmee Belgen wekelijks met hun GSM het meest online actief zijn.

Geef deze % weer in een staafdiagram zoals het voorbeeld hieronder; maak gebruik van de gegevens en zorg zelf voor de titels van de beide assen alsook van de vermelding van de gegevens zelf (titel, waarden en onderdelen x).